Un quaternion est un type de nombre hypercomplexe, mis en forme au XIXe siècle, par Hamilton qui cherchait à construire un ensemble de nombres ayant, dans l’espace, des propriétés analogues à celles que possèdent les nombres complexes dans le plan.
Les quaternions permettent d’étendre la notion de rotation en 3 dimensions à celle en 4 dimensions. Ils permettent ainsi d’éviter le gimbal lock (Blocage de cardan: voir particulièrement la perte d’un degré de liberté avec les angles d’Euler) et l’implémentation de rotations plus continues et plus précises.
Avant d’entrer plus le détail, vous devez vous demander, mais pourquoi utiliser les quaternions, les rotations c’est déjà bien non ? Les rotations d’Euler sont pratiques… en théorie. En utilisation réelle, on a souvent besoin de faire des rotations par rapport à un axe quelconque, et là, les quaternions sont très utiles. Les quaternions offrent aussi l’avantage de permettre l’interpolation. Ceci permet des rotations plus souples et plus réalistes.
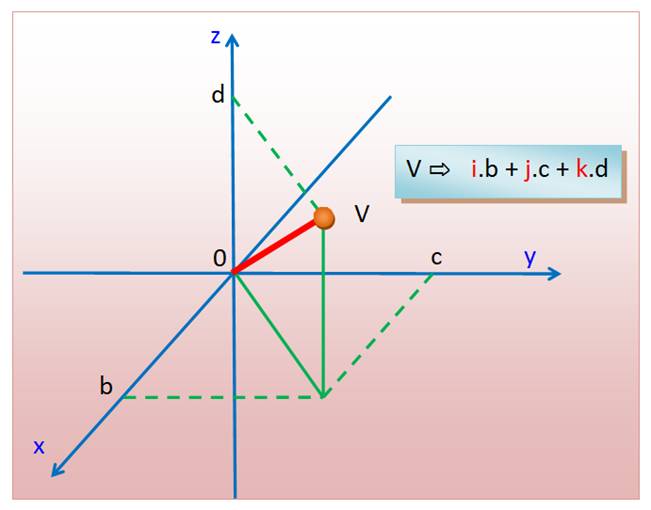
Un quaternion est défini via l’usage de 4 valeurs réelles (x, y, z, w). Elles sont calculées par une combinaison des 3 coordonnées de l’axe de rotation et de l’angle correspondant.

 Pour les calculs mathématiques et les conversions, je vous renvoie vers l’excellente FAQ sur developpez.com
Pour les calculs mathématiques et les conversions, je vous renvoie vers l’excellente FAQ sur developpez.com




0 commentaires