Bon, vous vous doutez bien que ce n’est pas en un article que nous allons faire le tour des fractales. Mon objectif, c’est de vous expliquer ce qu’est une fractale et comment on peut la dessiner en programmation. Après, c’est un domaine vaste et passionnant qui peut être utilisé dans de nombreux domaines – et nous y reviendrons! Mais pour l’instant, contentons nous de découvrir les mathématiques derrières les fractales et leur représentation graphique.
Voici un vidéo exceptionnelle tellement qu’elle est bien faite ! 😉 Non, sérieusement, penchez-vous 9 minutes là dessus et vous allez tout comprendre, même si vous n’êtes pas bon en math:
D’ailleurs, j’en profite pour vous glisser un petit mot sur cette chaine « El Jj » – plus connu sous le nom de « choux romanesco » (on comprend qu’il s’intéresse aux fractales) qui propose un contenu très intéressant pour ceux qui s’intéressent un peu aux maths, mais qui n’ont pas eu la chance de faire un doctorat dans le domaine 😉
Bon grâce à cette vidéo (ou votre expérience) vous comprenez ici comment on dessine une fractale. Que vous soyez familier ou non de python, je vous propose un petit exemple tout simple:
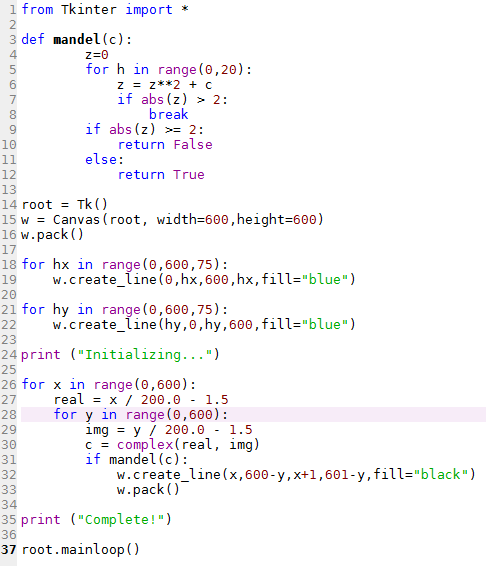
On peut difficilement faire plus simple non ? Pour le tester, il suffit de mettre ce code dans un fichier mandelbrot.py par exemple, d’installer python, et de lancer la commande « python mandelbrot.py ». Vous pouvez télécharger le script ici.
Voici ce que cela donne:

Expliquons maintenant ce que nous venons de faire:
Dans un premier temps,nous utilisons la librairie Tk pour créer une fenêtre graphique de 600×600 et nous traçons des lignes (on aurait même pu s’en passer).
Puis pour chaque pixel (point de l’image) :
- nous définissons un réel qui va aller de -1.5 à 1.5 (représenté en x) et un imaginaire entre -1.5 et 1.5 également (représenté en y).
- Nous créons un nombre complexe c à partir de ces deux valeurs
- Nous appelons une fonction mandel() en passant ce nombre complexe qui va vérifier si ce nombre génère une suite bornée ou non (voir vidéo).
- Si la suite est bornée alors on trace le point (ne vous inquiétez pas pour ce create_line, c’est juste qu’on ne peut pas tracer un point autrement sous Tk – c’est con mais c’est comme ça).
Comment fonctionne mandel() ?
Elle prend un complexe en paramètre d’entrée.Elle réalise un petit calcul tout simple en partant de z = 0, elle applique z = z² + c . Pour vérifier si la suite est bornée ou non, elle répète l’opération 20 fois : ici, cela suffit largement. Si on s’éloigne de (-2;2), on considère que la suite est non-bornée.
Voilà, ce n’est pas plus compliqué et cela dessine ce que nous avons vu précédemment.
Ne trouvez-vous pas tout cela extraordinaire ? N’êtes-vous pas fasciné comme moi par ce que nous découvrons ici.. un univers qui semble hyper-riche… et pourtant basé sur une formule des plus simples: z = z² + c !
Dans ce blog, nous poursuivrons l’étude des fractales, mais pas juste pour faire joli… nous les explorerons en 3D dans un premier temps, mais ensuite, nous verrons comment s’en servir pour trouver des solutions à des phénomènes complexes (sans jeu de mot). Su vous n’avez pas lu mon article sur l’utilisation des fractales en bourse et si vous avez une heure à tuer, c’est ici.




Je n’aurais pas pensé que c’était si simple… merci pour le démonstration !