L’algorithme de recherche A* (A star) est un algorithme de recherche de chemin dans un graphe entre un nœud initial et un nœud final tous deux donnés. De par sa simplicité il est souvent présenté comme exemple typique d’algorithme utilisé en intelligence artificielle. L’algorithme A* a été créé pour que la première solution trouvée soit l’une des meilleures, c’est pourquoi il est célèbre dans des applications comme les jeux vidéo privilégiant la vitesse de calcul sur l’exactitude des résultats. Cet algorithme a été proposé pour la première fois par Peter E. Hart, Nils Nilsson et Bertram Raphael en 1968. Il s’agit d’une extension de l’algorithme de Dijkstra de 1959.
Algorithme
A chaque itération, A* va tenter de prendre le chemin le plus court pour aller d’une position Src à une position Dst.
Pour déterminer si un nœud est suceptible de faire partie du chemin solution, il faut pouvoir quantifier sa qualité. Le plus souvent, on utilise la distance en « vol d’oiseau » entre la position du noeud et Dst, mais d’autres fonctions peuvent être utilisées.
On travaille à partir d’une position de départ, d’une arrivée, d’un terrain, et de deux listes de nœuds (ouverte et fermée), vides à l’origine.
- A partir du départ, on regarde quels sont les nœuds voisins (correspondant aux libertés de mouvement – Par exemple, on peut aller à droite, à gauche, sauter ou ramper, reculer ou avancer – 6 possibilités = 6 noeuds). On place le nœud de départ dans la liste fermée.
- Pour chaque nœud voisin :
- Si c’est un obstacle, on passe (on ne traite pas ce nœud, il ne sera ajouté nulle part)
- S’il est déjà dans la liste fermée, on passe (on a déjà étudié ce trajet)
- S’il est déjà dans la liste ouverte, On vérifie sa qualité. Si la qualité actuelle est meilleure, c’est que le chemin est plus court en passant par le trajet actuel, donc on met à jour sa qualité dans la liste ouverte, et on met à jour son lien parent (avec noeud courant qui correspond à un meilleur chemin)
- Sinon, on ajoute ce nœud à la liste ouverte avec comme parent le nœud courant
- On parcours la liste ouverte à la recherche du nœud ayant la meilleure qualité. Si la liste ouverte est vide, il n’y a pas de solution, fin de l’algorithme.
- On prend le meilleur, et on le retire de la liste ouverte pour le mettre dans la liste fermée
- Nœud courant = nœud qu’on vient d’insérer
- Si nœud courant = Dst alors c’est bon, on a trouvé un bon chemin, sinon on réitère en 2.
La liste ouverte contient toutes les pistes de trajet qui sont encore possibles. La liste fermée contient toutes les solutions étudiées, bonnes et mauvaises.
Le « bon chemin » trouvé se retrouve en remontant le long des parents de nœuds.
Implémentation sous Python
Vous pouvez télécharger le code source de la classe, ainsi que le code source de l’exemple à partir de l’archive suivante.
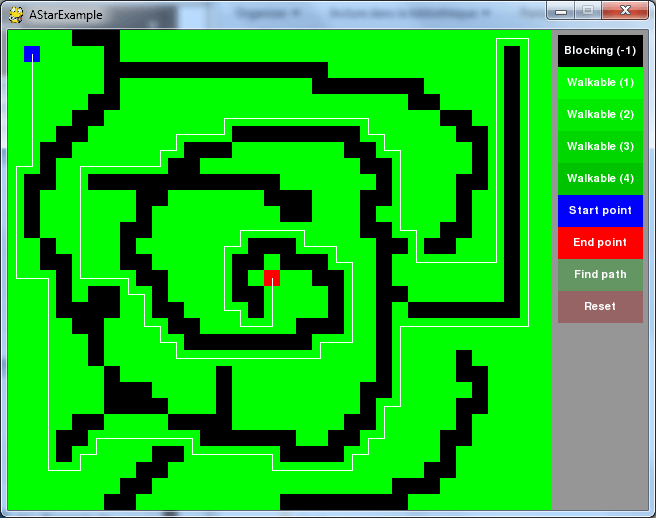 La classe Astar est générique, elle est implémentée au travers de SQ_MapHandler :
La classe Astar est générique, elle est implémentée au travers de SQ_MapHandler :
astar = AStar.AStar(AStar.SQ_MapHandler(self.mapdata,self.mapw,self.maph))
Elle peut facilement être adaptée et réutilisée pour d’autres sujet..
Le déplacement n’est assuré qu’au travers de Haut,Bas,Droite,Gauche du membre getAdjacentNodes() de SQ_MapHandler. La fonction renvoi une liste des nœuds possibles.
La qualité est calculée par SQ_MapHandler._handleNode():
dx = max(x,destx) - min(x,destx) dy = max(y,desty) - min(y,desty) emCost = dx+dy n.mCost += fromnode.mCost n.score = n.mCost+emCost
Il y a ici deux notions de qualité: le walkable et la distance. Un calcul permet de gérer les 2 valeurs.
C’est la classe Astar._getBestOpenNode() qui effectue la recherche du meilleur candidat (nœud ayant la meilleure qualité): ce sont les scores qui sont comparés et le plus petit représente le meilleur.
La fonction principale qui étudie un nœud voisin en phase 2 de l’algo est la suivante:
def _handleNode(self,node,end):
i = self.o.index(node.lid)
self.on.pop(i)
self.o.pop(i)
self.c.append(node.lid)
nodes = self.mh.getAdjacentNodes(node,end)
for n in nodes:
if n.location == end:
# reached the destination
return n
elif n.lid in self.c:
# already in close, skip this
continue
elif n.lid in self.o:
# already in open, check if better score
i = self.o.index(n.lid)
on = self.on[i];
if n.mCost & on.mCost:
self.on.pop(i);
self.o.pop(i);
self.on.append(n);
self.o.append(n.lid);
else:
# new node, append to open list
self.on.append(n);
self.o.append(n.lid);
return None
Liste ouverte (self.o) et fermée (self.c) ne sont composées que des positions (node.lid) des différents nœuds.Seule la liste ouverte possède (self.on) possède une liste de nodes. Chaque node est représenté par une position (x,y), un lid unique (position. Ex: y*taillex+x), un coût, un score et un parent. Nodes réccupère ensuite la liste des nœuds adjacents possibles et pour chaque nœud adjacent un traitement est effectué. Si on est arrivé à destination alors on retourne le nœud. Sinon, s’il est déjà en liste fermée, on passe. S’il est en liste ouverte, on le retrouve et si le cout actuel (cost) est meilleur que celui en liste ouverte, alors on le retire de la liste et on le remplace par celui actuel. Sinon, on l’ajoute à la liste ouverte.
La recherche du plus court chemin se fait donc par la fonction Astar.findPath():
def findPath(self,fromlocation, tolocation):
self.o = []
self.on = []
self.c = []
end = tolocation
fnode = self.mh.getNode(fromlocation)
self.on.append(fnode)
self.o.append(fnode.lid)
nextNode = fnode
while nextNode is not None:
finish = self._handleNode(nextNode,end)
if finish:
return self._tracePath(finish)
nextNode=self._getBestOpenNode()
return None
Elle initialise les 3 listes précédente, puis définit la propriété end avec la destination. Fnode est initialisé avec le nœud de départ, qu’on ajoute en liste ouverte. Le nœud courant devient alors le nœud de départ et on lance une boucle dans laquelle, tant que le prochain nœud n’est pas vide, on le traite avec la fonction _handleNode et on choisit le prochain meilleur dans la liste ouverte avec _getBestOpenNode().
C’est bien là le cœur du traitement.
Une fois le chemin trouvée, on peut l’afficher grâce à Astar._tracePath()
def _tracePath(self,n):
nodes = [];
totalCost = n.mCost;
p = n.parent;
nodes.insert(0,n);
while 1:
if p.parent is None:
break
nodes.insert(0,p)
p=p.parent
return Path(nodes,totalCost)
Voici une vidéo de P. Armand expliquant l’algorithme pas à pas:
Cet article est un peu ancien, depuis nous traitons de ces sujets dans le cadre d’un magazine. Regardez cette vidéo pour savoir si ce mag est fait pour vous !





Le code source est indisponible
Voilà qui est corrigé!